Gradien dan Persamaan Garis - Kelas 8 SMP
Soal No. 1
Diberikan 4 buah garis dalam koordinat cartesius seperti terlihat pada gambar berikut.
Tentukan gradien dari keempat garis pada gambar di bawah.


Pembahasan
Untuk menentukan gradien dari suatu garis
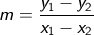
dimana
m = gradien atau kemiringan garis
I) Misal titik 1 adalah (x1, y1) = (3, 0) dan titik 2 (x2, y2) = (0, 6)
masuk formula m diatas sehingga
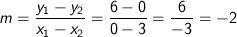
Bagaimana jika titik 1 dan 2 nya diambil secara berkebalikan? Coba kita lihat
Misal titik 1 adalah (x1, y1) = (0, 6) dan titik 2 (x2, y2) = (3, 0) masukkan rumus yang sama dengan angka yang telah kita balik tadi
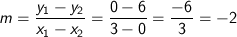
Ternyata hasilnya adalah sama, jadi ambil saja sembarang tak perlu pusing dengan mana titik satu mana titik 2.
II) Titik-titik yang diketahui dari gambar adalah (0, 6) dan (−3, 0) sehingga gradien garisnya adalah
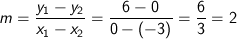
III) Titik-titik yang diketahui dari gambar adalah (−3, 0) dan (0, −6) sehingga gradien garisnya adalah
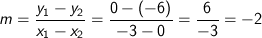
IV) Titik-titik yang diketahui dari gambar adalah (3, 0) dan (0, −6) sehingga gradien garisnya adalah
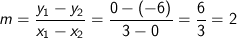
Soal No. 2
Tentukan persamaan garis yang memiliki gradien 3 dan melalui titik:
a) (3, 6)
b) (-4, 5)
Pembahasan
Menentukan persamaan suatu garis lurus jika telah diketahui gradiennya dengan cukup satu titik yang diketahui:
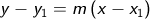
Masukkan angkanya didapatkan hasil
a) Melalui titik (3, 6)
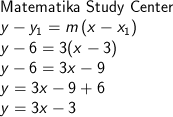
b) Melalui titik (-4, 5)

Soal No. 3
Tentukan persamaan garis yang melalui titik (3, 4) dan titik (5, 12)!
Pembahasan
Menentukan persamaan suatu garis lurus jika diketahui dua buah titik yang dilaluinya:
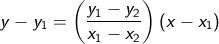
masukkan, dengan titik (5, 12)
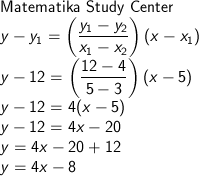
atau, dengan titik (3, 4), dimana hasilnya haruslah sama,
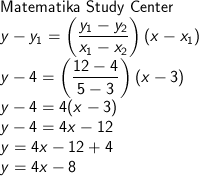
Soal No. 4
Tentukan gradien dari persamaan garis-garis berikut:
a) y = 3x + 2
b) 10x − 6y + 3 = 0
Pembahasan
a) y = 3x + 2
Pola persamaan garis pada soal a adalah
y = mx + C
Sehingga dengan mudah menemukan gradien garisnya m = 3
b) 18x − 6y + 24 = 0
Ubah persamaan b menjadi pola y = mx + c
18x − 6y + 24 = 0
18x + 24 = 6y
6y = 18x + 24
bagi dengan angka 6
y = 3x + 4
sehingga m = 3
Untuk menentukan gradien dari suatu garis
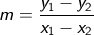
dimana
m = gradien atau kemiringan garis
I) Misal titik 1 adalah (x1, y1) = (3, 0) dan titik 2 (x2, y2) = (0, 6)
masuk formula m diatas sehingga
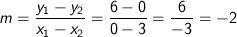
Bagaimana jika titik 1 dan 2 nya diambil secara berkebalikan? Coba kita lihat
Misal titik 1 adalah (x1, y1) = (0, 6) dan titik 2 (x2, y2) = (3, 0) masukkan rumus yang sama dengan angka yang telah kita balik tadi
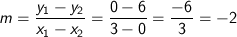
Ternyata hasilnya adalah sama, jadi ambil saja sembarang tak perlu pusing dengan mana titik satu mana titik 2.
II) Titik-titik yang diketahui dari gambar adalah (0, 6) dan (−3, 0) sehingga gradien garisnya adalah
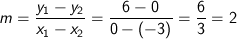
III) Titik-titik yang diketahui dari gambar adalah (−3, 0) dan (0, −6) sehingga gradien garisnya adalah
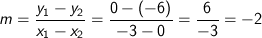
IV) Titik-titik yang diketahui dari gambar adalah (3, 0) dan (0, −6) sehingga gradien garisnya adalah
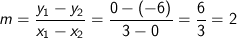
Soal No. 2
Tentukan persamaan garis yang memiliki gradien 3 dan melalui titik:
a) (3, 6)
b) (-4, 5)
Pembahasan
Menentukan persamaan suatu garis lurus jika telah diketahui gradiennya dengan cukup satu titik yang diketahui:
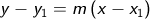
Masukkan angkanya didapatkan hasil
a) Melalui titik (3, 6)
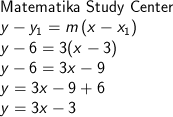
b) Melalui titik (-4, 5)

Soal No. 3
Tentukan persamaan garis yang melalui titik (3, 4) dan titik (5, 12)!
Pembahasan
Menentukan persamaan suatu garis lurus jika diketahui dua buah titik yang dilaluinya:
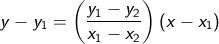
masukkan, dengan titik (5, 12)
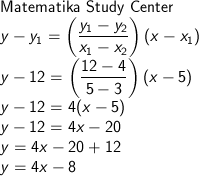
atau, dengan titik (3, 4), dimana hasilnya haruslah sama,
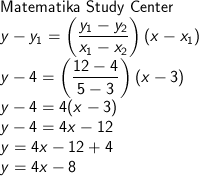
Soal No. 4
Tentukan gradien dari persamaan garis-garis berikut:
a) y = 3x + 2
b) 10x − 6y + 3 = 0
Pembahasan
a) y = 3x + 2
Pola persamaan garis pada soal a adalah
y = mx + C
Sehingga dengan mudah menemukan gradien garisnya m = 3
b) 18x − 6y + 24 = 0
Ubah persamaan b menjadi pola y = mx + c
18x − 6y + 24 = 0
18x + 24 = 6y
6y = 18x + 24
bagi dengan angka 6
y = 3x + 4
sehingga m = 3
Soal No. 5
Tentukan persamaan garis yang melalui titik (3, 1) dan tegak lurus dengan garis y = 2x + 5
Pembahasan
Dua buah garis saling tegak lurus jika memenuhi syarat sebagai berikut
m1 ⋅ m2 = −1
y = 2x + 5 memiliki gradien m1 = 2, sehingga garis yang akan dicari persamaannya harus memiliki gradien
m1 ⋅ m2 = −1
2 ⋅ m2 = −1
m2 = − 1/2
Tinggal disusun persamaan garisnya
y − y1 = m(x − x1)
y − 1 = 1/2(x − 3)
y − 1 = 1/2 x − 3/2
y = 1/2 x − 3/2 + 1
y = 1/2 x − 1/2
Soal No. 6
Tentukan persamaan garis yang melalui titik (3, 1) dan sejajar dengan garis y = 2x + 5
Pembahasan
Dua buah garis yang sejajar memiliki syarat gradiennya harus sama atau
m1 = m2
Gradien garis y = 2x + 5 adalah 2, sehingga gradien garis yang akan dicari juga 2 karena mereka sejajar. Sehingga
y − y1 = m(x − x1)
y − 1 = 2 (x − 3)
y − 1 = 2x − 6
y = 2x − 6 + 1
y = 2x − 5
Tentukan persamaan garis yang melalui titik (3, 1) dan tegak lurus dengan garis y = 2x + 5
Pembahasan
Dua buah garis saling tegak lurus jika memenuhi syarat sebagai berikut
m1 ⋅ m2 = −1
y = 2x + 5 memiliki gradien m1 = 2, sehingga garis yang akan dicari persamaannya harus memiliki gradien
m1 ⋅ m2 = −1
2 ⋅ m2 = −1
m2 = − 1/2
Tinggal disusun persamaan garisnya
y − y1 = m(x − x1)
y − 1 = 1/2(x − 3)
y − 1 = 1/2 x − 3/2
y = 1/2 x − 3/2 + 1
y = 1/2 x − 1/2
Soal No. 6
Tentukan persamaan garis yang melalui titik (3, 1) dan sejajar dengan garis y = 2x + 5
Pembahasan
Dua buah garis yang sejajar memiliki syarat gradiennya harus sama atau
m1 = m2
Gradien garis y = 2x + 5 adalah 2, sehingga gradien garis yang akan dicari juga 2 karena mereka sejajar. Sehingga
y − y1 = m(x − x1)
y − 1 = 2 (x − 3)
y − 1 = 2x − 6
y = 2x − 6 + 1
y = 2x − 5
Soal No. 7
Garis p memiliki persamaan :
y = 2x + 5
Tentukan persamaan garis yang didapatkan dengan:
a) menggeser garis p ke atas sebanyak 3 satuan
b) menggeser garis p ke bawah sebanyak 3 satuan
Pembahasan
Pergeseran suatu garis ke atas dan ke bawah.
y = 2x + 5
a) digeser ke atas sebanyak 3 satuan menjadi:
y = 2x + 5 + 3
y = 2x + 8
b) digeser ke bawah sebanyak 3 satuan
y = 2x + 5 − 3
y = 2x + 2
Soal No. 8
Garis m memiliki persamaan :
y = 2x + 10
Tentukan persamaan garis yang didapatkan dengan:
a) menggeser garis m ke kanan sebanyak 3 satuan
b) menggeser garis m ke kiri sebanyak 3 satuan
Pembahasan
Pergeseran suatu garis ke kanan dan ke kiri.
y = 2x + 10
a) digeser ke kanan sebanyak 3 satuan
y = 2(x − 3) + 10
y = 2x − 6 + 10
y = 2x + 4
b) digeser ke kiri sebanyak 3 satuan
y = 2(x + 3) + 10
y = 2x + 6 + 10
y = 2x + 16
Soal No. 9
Garis y = 1/2 x − 5 sejajar dengan garis yang melalui titik P (10, a + 4) dan titik Q (a, 8). Tentukan koordinat dari titik P dan titik Q!
Pembahasan
Gradien garis y = 1/2 x − 5 adalah 1/2. Dua garis yang sejajar memiliki gradien yang sama. Sehingga gradien garis PQ juga 1/2.

Koordinat titik P = (10, a + 4) = (10, 6 + 4) = (10, 10)
Koordinat titik Q = (a, 8) = (6, 8)
Garis p memiliki persamaan :
y = 2x + 5
Tentukan persamaan garis yang didapatkan dengan:
a) menggeser garis p ke atas sebanyak 3 satuan
b) menggeser garis p ke bawah sebanyak 3 satuan
Pembahasan
Pergeseran suatu garis ke atas dan ke bawah.
y = 2x + 5
a) digeser ke atas sebanyak 3 satuan menjadi:
y = 2x + 5 + 3
y = 2x + 8
b) digeser ke bawah sebanyak 3 satuan
y = 2x + 5 − 3
y = 2x + 2
Soal No. 8
Garis m memiliki persamaan :
y = 2x + 10
Tentukan persamaan garis yang didapatkan dengan:
a) menggeser garis m ke kanan sebanyak 3 satuan
b) menggeser garis m ke kiri sebanyak 3 satuan
Pembahasan
Pergeseran suatu garis ke kanan dan ke kiri.
y = 2x + 10
a) digeser ke kanan sebanyak 3 satuan
y = 2(x − 3) + 10
y = 2x − 6 + 10
y = 2x + 4
b) digeser ke kiri sebanyak 3 satuan
y = 2(x + 3) + 10
y = 2x + 6 + 10
y = 2x + 16
Soal No. 9
Garis y = 1/2 x − 5 sejajar dengan garis yang melalui titik P (10, a + 4) dan titik Q (a, 8). Tentukan koordinat dari titik P dan titik Q!
Pembahasan
Gradien garis y = 1/2 x − 5 adalah 1/2. Dua garis yang sejajar memiliki gradien yang sama. Sehingga gradien garis PQ juga 1/2.

Koordinat titik P = (10, a + 4) = (10, 6 + 4) = (10, 10)
Koordinat titik Q = (a, 8) = (6, 8)
Soal No. 10
Tentukan persamaan garis berikut dengan cepat!

Pembahasan
Menentukan persamaan garis dengan diketahui titik potongnya pada sumbu x dan sumbu y:
Tentukan persamaan garis berikut dengan cepat!

Pembahasan
Menentukan persamaan garis dengan diketahui titik potongnya pada sumbu x dan sumbu y:
bx + ay = ab
a itu angka disumbu x, yang memotong tentunya,
b itu angka di sumbu y
ab maksudnya a dikali b.
dari gambar:
a = 3
b = 2
Jadi persamaan garisnya:
2x + 3y = 6
a = 3
b = 2
Jadi persamaan garisnya:
2x + 3y = 6
Soal No. 11
Gradien garis x − 3y = − 6 adalah....
A. −3
B. − 1/3
C. 1/3
D. 3
(Gradien dan Persamaan Garis - un matematika smp 2012)
Pembahasan
Cara pertama
Arahkan ke bentuk umum persamaan garis, dengan m adalah gradien
Gradien garis x − 3y = − 6 adalah....
A. −3
B. − 1/3
C. 1/3
D. 3
(Gradien dan Persamaan Garis - un matematika smp 2012)
Pembahasan
Cara pertama
Arahkan ke bentuk umum persamaan garis, dengan m adalah gradien
| y = mx + c |
x − 3y = − 6
x + 6 = 3y
3y = x + 6
y = x/3 + 6/3
y = 1/3 x + 2
Jadi m = 1/3
Cara kedua
Satukan x dan y dalam satu ruas, boleh di kiri semua atau di kanan semua, pada soal di atas x dan y sudah dalam satu ruas. Kemudian

Soal:
x − 3y = − 6
koefisien x = 1
koefisien y = −3
Jadi
m = − koefisien x / koefisien y
= − 1 / −3
= 1/3
Catatan:
Perhatikan perbedaan rumusnya dengan soal nomor 1.
Soal No.12
Gradien garis dengan persamaan 3x + 8y = 9 adalah...
A. 8/3
B. 3/8
C. −3/8
D. −8/3
(UN SMP 2013)
Pembahasan
Seperti nomor 11 dengan cara kedua:
m = − 3/8
Komentar
Posting Komentar