Integral Kalkulus
Rumus Dasar
Teori Singkat
Rumus integral tak tentu
Rumus integral tak tentu
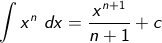 |
Soal
Tentukan:
1) ∫ x5 dx
2) ∫ 3√x dx
3) ∫ dx/x5
4) ∫ y5 dy
5) ∫ √t dt
6) ∫ (3x2 + 5x) dx
7) ∫ ( 1/4 x4 + 1/3 x3 + 1/2 x2) dx
8) ∫ (2x − 1)2 dx
Pembahasan
1) Penggunaan rumus dasar integral
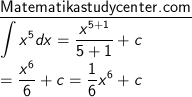
2) Penggunaan rumus dasar integral
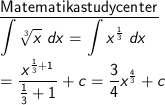
3) Penggunaan rumus dasar integral
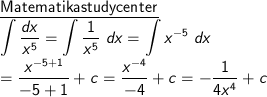
4) Penggunaan rumus dasar integral
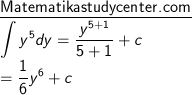
5) Penggunaan rumus dasar integral
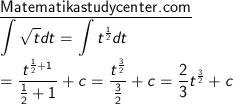
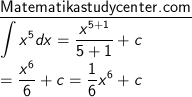
2) Penggunaan rumus dasar integral
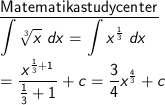
3) Penggunaan rumus dasar integral
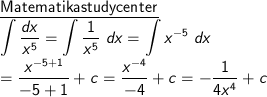
4) Penggunaan rumus dasar integral
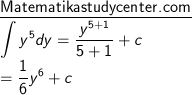
5) Penggunaan rumus dasar integral
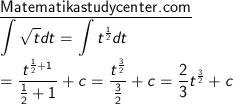
6) Penggunaan rumus dasar integral
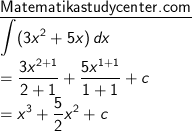
7) Penggunaan rumus dasar integral
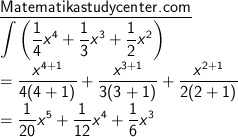
8) Penggunaan rumus dasar integral
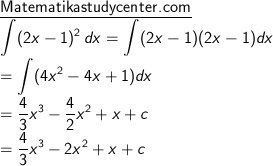
Integral dengan Substitusi Aljabar
Teori Singkat
Cermati rumus untuk integral dengan substitusi aljabar berikut, cara panjang akan diberikan di pembahasan contoh soal.
Cermati rumus untuk integral dengan substitusi aljabar berikut, cara panjang akan diberikan di pembahasan contoh soal.
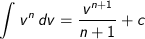 |
c adalah konstanta.
Soal No. 1
Tentukan:
∫ (3x + 7)5 dx
Pembahasan
Bawa ke bentuk ∫ vn dv
Misal:
v = (3x + 5) dengan demikian:
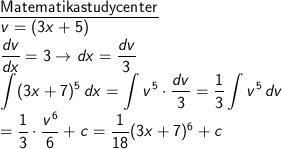
Misal:
v = (3x + 5) dengan demikian:
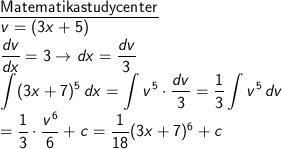
Soal No. 2
Tentukan dengan menggunakan metode substitusi aljabar :
∫ (2x + 10)3 dx
Pembahasan
∫ (2x + 10)3 dx
Pembahasan
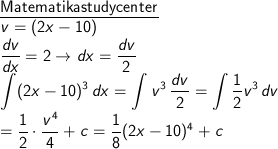
Soal No. 3
Tentukan hasil dari:
∫ √(3x + 6) dx
Pembahasan
∫ √(3x + 6) dx
Pembahasan
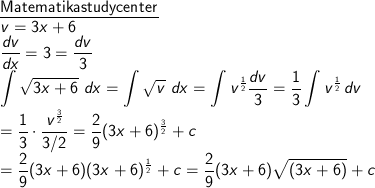
Soal No. 4
Tentukan hasil dari:
∫ 3√(3x + 6) dx
Pembahasan
Tentukan hasil dari:
∫ 3√(3x + 6) dx
Pembahasan
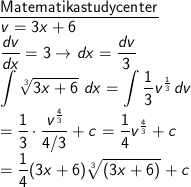
Soal No. 5
Tentukan hasil dari:
∫ (3x3 + 5)7 x2 dx
Pembahasan
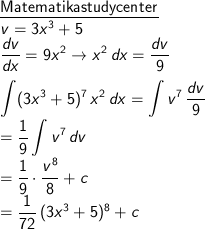
Soal No. 5
Tentukan hasil dari:
∫ 3√(12 x5 − 7) x4 dx
Pembahasan
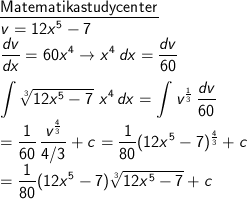
Soal No. 7
Hasil dari
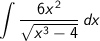
adalah....
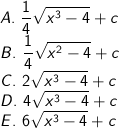
Sumber soal : Ebtanas Matematika 1999
Pembahasan
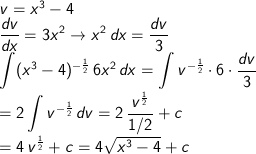
Hasil dari
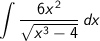
adalah....
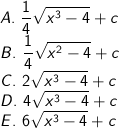
Sumber soal : Ebtanas Matematika 1999
Pembahasan
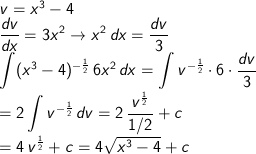
 Integral Trigonometri
Integral Trigonometri
Penggunaan rumus dasar integral trigonometri untuk penyelesaian soal, sinus, cosinus dan secan.
Soal-Soal:
Tentukan:
1) ∫ 5 cos x dx
2) ∫ − 6 sin x dx
3) ∫ 7 sec2 x dx
4) ∫ −( 8/cos 2 x ) dx
5) ∫ (10 cos x − 9 sin x) dx
6) ∫ 2 cos x tan x dx
7) ∫ ( 4/1 − sin 2 x ) dx
8) ∫ √(16 − 16 sin2 x) dx
1) ∫ 5 cos x dx
2) ∫ − 6 sin x dx
3) ∫ 7 sec2 x dx
4) ∫ −( 8/cos 2 x ) dx
5) ∫ (10 cos x − 9 sin x) dx
6) ∫ 2 cos x tan x dx
7) ∫ ( 4/1 − sin 2 x ) dx
8) ∫ √(16 − 16 sin2 x) dx
Teori Singkat
Cermati rumus-rumus dasar integral untuk fungsi-fungsi trigonometri berikut:
Cermati rumus-rumus dasar integral untuk fungsi-fungsi trigonometri berikut:
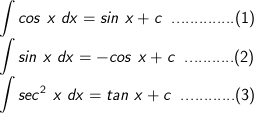 |
Pembahasan
1) Dengan rumus (1), keluarkan angka 5 dari integral didapat hasil :
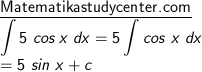
1) Dengan rumus (1), keluarkan angka 5 dari integral didapat hasil :
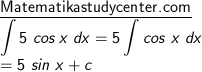
2) Keluarkan -6 dari integral, kemudian pergunakan rumus (2):
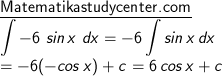
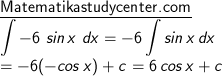
3) Gunakan rumus (3):
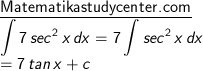
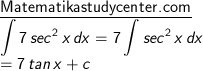
4) Ingat kembali bahwa cos x adalah kebalikan dari sec x, kemudian masuk ke pola (3):
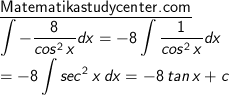
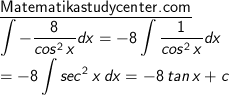
5) Gabungan integral untuk sin x dan cos x:
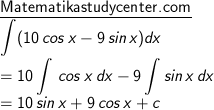
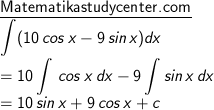
6) tan x tidak ada pada pola kita di atas, ingat kembali bahwa
tan x = sin x / cos x
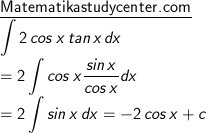
7) Ingat identitas trigonometri berikut :
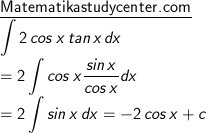
7) Ingat identitas trigonometri berikut :
sin2 x + cos 2 x = 1
Sehingga
1 - sin 2 x = cos 2 x dan cos x adalah kebalikan dari sec x
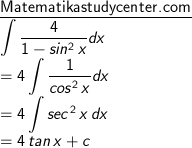
8) Arahkan soal hingga mendapat bentuk dalam sin x :
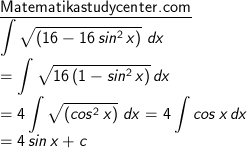
Integral Trigonometri Sin (ax+b)
Contoh soal dan pembahasan jawaban materi integral , matematika kelas 12 SMA, penggunaan rumus dasar integral trigonometri untuk penyelesaian soal, sin (ax + b), cos (ax + b) dan sec2 (a + b).
Soal-soal
Tentukan:
1) ∫ sin 3x dx
2) ∫ 2 sin 3x dx
3) ∫ sin (3x + 2) dx
4) ∫ sin (3x − 1/2 π ) dx
5) ∫ cos 5x dx
6) ∫ cos (5x−3) dx
7) ∫ sec2 5x dx
8) ∫ sec2 (2x+3) dx
Teori singkat
Cermati rumus-rumus dasar integral untuk fungsi-fungsi trigonometri untuk sudut-sudut berikut:
Teori singkat
Cermati rumus-rumus dasar integral untuk fungsi-fungsi trigonometri untuk sudut-sudut berikut:
 |
Pembahasan
1) Dengan rumus sin ax, a = 3
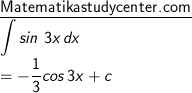
2) Dengan rumus sin ax, a = 3, keluarkan 2 dari integral:
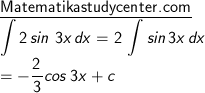
3) Dengan rumus sin (ax + b), a = 3 dan b = 2
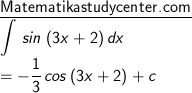
4) Dengan rumus sin (ax + b), dimana a = 3 dan b = − 1/2 π
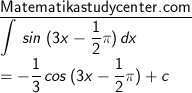
5) Dengan rumus cos ax, dimana a = 5
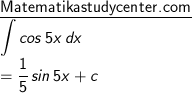
6) Dengan rumus cos (ax + b), dimana a = 5 dan b = -3
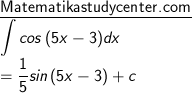
7) Dengan rumus sec2 ax, dimana a = 5
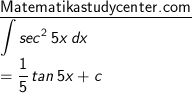
8) Dengan rumus sec2 (ax + b), dimana a = 2 dan b = 3
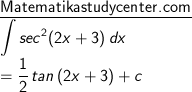
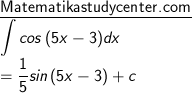
7) Dengan rumus sec2 ax, dimana a = 5
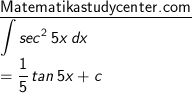
8) Dengan rumus sec2 (ax + b), dimana a = 2 dan b = 3
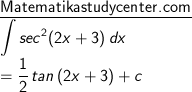
Integral Substitusi Trigonometri
Pola rumus yang digunakan untuk soal-soal integral trigonometri dengan teknik substitusi diantaranya

Asumsinya adik-adik tidak menemui kesulitan dalam hal turunan fungsi trigonometri, misalnya turunan dari sin 3x jadinya apa, atau turunan dari cos 5x seperti apa jadinya, jika lupa bagaimana turunan suatu fungsi trigonometri silakan diulang lagi, atau sambil buka buku catatan.
Rumus lainnya:


Soal No. 1
Hasil dari:
∫ cos3 3x sin 3x dx
adalah....
Hasil dari:
∫ cos3 3x sin 3x dx
adalah....
(Modifikasi UN 2011)
Pembahasan
Buat dulu permisalannya:
v = cos 3x
Turunkan v nya:
dv/dx = −3 sin 3x
sehingga jika diperlukan dx
dx = dv/−3 sin 3x

Kembali ke soal, sambil memasukkan permisalan tadi, ganti cos 3x dengan v dan dx dengan dv/−3 sin 3x, sin 3x biarkan saja, nanti bisa dicoret, Sehingga

Kembalikan v jadi cos 3x lagi

Soal No. 2
Hasil dari ∫ cos2 x sin x dx adalah....
A. 1/3 cos3 x + C
B. − 1/3 cos3 x + C
C. − 1/3 sin3 x + C
D. 1/3 sin3 x + C
E. 3 sin3 x + C
(Integral Substitusi Trigonometri - UN 2008)
Pembahasan
Setipe dengan contoh pertama, misalkan:
v = cos x
Menemukan dx nya

Pasang lagi

Soal No. 3
Hasil dari
∫ 5x sin x2 dx = ....
(Modifikasi UAN 2006)
Pembahasan
Berbeda tipe dengan dua soal sebelumnya. Jika sebelumnya sin atau cos nya yang dipangkat, yang ini x di dalam yang dipangkatkan.
Pembahasan
Buat dulu permisalannya:
v = cos 3x
Turunkan v nya:
dv/dx = −3 sin 3x
sehingga jika diperlukan dx
dx = dv/−3 sin 3x

Kembali ke soal, sambil memasukkan permisalan tadi, ganti cos 3x dengan v dan dx dengan dv/−3 sin 3x, sin 3x biarkan saja, nanti bisa dicoret, Sehingga

Kembalikan v jadi cos 3x lagi

Soal No. 2
Hasil dari ∫ cos2 x sin x dx adalah....
A. 1/3 cos3 x + C
B. − 1/3 cos3 x + C
C. − 1/3 sin3 x + C
D. 1/3 sin3 x + C
E. 3 sin3 x + C
(Integral Substitusi Trigonometri - UN 2008)
Pembahasan
Setipe dengan contoh pertama, misalkan:
v = cos x
Menemukan dx nya

Pasang lagi

Soal No. 3
Hasil dari
∫ 5x sin x2 dx = ....
(Modifikasi UAN 2006)
Pembahasan
Berbeda tipe dengan dua soal sebelumnya. Jika sebelumnya sin atau cos nya yang dipangkat, yang ini x di dalam yang dipangkatkan.
Misalkan x2 sebagai v.

pasang v dan dx nya, biarkan saja 5x nya

Soal No. 4
∫ 2x cos (x2 + 1)dx = ....
Pembahasan
Misal:
v = x2 + 1
Jadi:

Kembali ke soal,

Ganti (x2 + 1) dengan v dan dx dengan dv/2x, sementara itu 2x biarkan saja, nanti dicoret:

Soal No. 5
∫sin3 x cos2 x dx =....
Pembahasan
Rumus bantu trigonometri berikut diperlukan:
cos2x + sin2x = 1
atau

pasang v dan dx nya, biarkan saja 5x nya

Soal No. 4
∫ 2x cos (x2 + 1)dx = ....
Pembahasan
Misal:
v = x2 + 1
Jadi:

Kembali ke soal,

Ganti (x2 + 1) dengan v dan dx dengan dv/2x, sementara itu 2x biarkan saja, nanti dicoret:

Soal No. 5
∫sin3 x cos2 x dx =....
Pembahasan
Rumus bantu trigonometri berikut diperlukan:
cos2x + sin2x = 1
atau
sin2x = 1 − cos2x
Kita edit soal diatas:
∫sin3x cos2x dx
= ∫sin2x sin x cos2x dx
= ∫[(1 − cos2x)sinx cos2x ]dx
= ∫[sinx cos2x − sinx cos4x]dx
= ∫ sinx cos2x dx − ∫sinx cos4x dx
Kemudian gunakan integral substitusi seperti soal-soal sebelumnya:
Misal cos x jadi v

Kembali ke soal, substitusikan

Kita edit soal diatas:
∫sin3x cos2x dx
= ∫sin2x sin x cos2x dx
= ∫[(1 − cos2x)sinx cos2x ]dx
= ∫[sinx cos2x − sinx cos4x]dx
= ∫ sinx cos2x dx − ∫sinx cos4x dx
Kemudian gunakan integral substitusi seperti soal-soal sebelumnya:
Misal cos x jadi v

Kembali ke soal, substitusikan

Integral Parsial
Berikut diberikan dua metode cara untuk menyelesaikan type soal integral parsial.
Ingat kembali rumus dasar untuk materi integral parsial sebagai berikut.
Rumus Dasar Integral Parsial
| ∫ u dv = uv − ∫v du |
Untuk lambang-lambangnya jika berbeda, silakan disesuaikan dengan literature atau buku yang adik-adik gunakan atau catatan yang diberikan Bapak Ibu Guru di sekolah masing-masing, pada prinsipnya sama saja.
Soal No. 1
Hasil dari 16 ∫ (x + 3) cos (2x − π)dx =.....
A. 8(2x + 6) sin (2x − π) + 4 cos (2x − π) + C
B. 8(2x + 6) sin (2x − π) − 4 cos (2x − π) + C
C. 8(x + 3) sin (2x − π) + 4 cos (2x − π) + C
D. 8(x + 3) sin (2x − π) − 4 cos (2x − π) + C
E. 8(x + 3) sin (2x − π) + 4 sin (2x − π) + C
Pembahasan
Beberapa cara biasa digunakan untuk menyelesaikan soal integral parsial, dua diantaranya akan ditunjukkan di sini.
Cara Pertama
∫ (x + 3) cos (2x − π)dx =.....
|____| |__________|
u dv
Hasil dari 16 ∫ (x + 3) cos (2x − π)dx =.....
A. 8(2x + 6) sin (2x − π) + 4 cos (2x − π) + C
B. 8(2x + 6) sin (2x − π) − 4 cos (2x − π) + C
C. 8(x + 3) sin (2x − π) + 4 cos (2x − π) + C
D. 8(x + 3) sin (2x − π) − 4 cos (2x − π) + C
E. 8(x + 3) sin (2x − π) + 4 sin (2x − π) + C
Pembahasan
Beberapa cara biasa digunakan untuk menyelesaikan soal integral parsial, dua diantaranya akan ditunjukkan di sini.
Cara Pertama
∫ (x + 3) cos (2x − π)dx =.....
|____| |__________|
u dv
Langkah pertama, tentukan dulu mana u mana dv
Misalkan (x + 3) adalah u, dan sisanya, cos (2x − π)dx sebagai dv,
u = (x + 3) ...(Persamaan 1)
dv = cos (2x − π)dx ...(Persamaan 2)
Langkah pertama selesai, kita tengok lagi rumus dasar integral parsial:
∫ u dv = uv − ∫v du
Terlihat di situ kita perlu u, perlu v dan perlu du. u nya sudah ada, tinggal mencari du dan v nya.
Dari persamaan 1, untuk menentukan du, caranya turunkan u nya,
u = (x + 3)
du/dx = 1
du = dx
Dari persamaan 2, untuk menentukan v,
dv = cos (2x − π)dx
atau
dv/dx = cos (2x − π)
dv/dx artinya turunan dari v adalah cos (2x − π), untuk mendapatkan v, berarti kita harus integralkan cos (2x − π) jika lupa, tengok lagi cara integral fungsi trigonometri,
v = ∫ cos (2x − π) dx = 1/2 sin (2x − π) + C
Kita rangkum lagi :
u = (x + 3)
v = 1/2 sin (2x − π)
du = dx
Saatnya kembali ke rumus dasar, masukkan nilai-nilai yang sudah dicari tadi:
16 ∫ (x + 3) cos (2x − π)dx
Simpan dulu 16 nya, terakhir nanti hasilnya baru di kali 16
= uv − ∫v du
= (x + 3) 1/2 sin (2x − π) − ∫ 1/2 sin (2x − π) du
= 1/2 (x + 3) sin (2x − π) − ∫ 1/2 sin (2x − π) dx
= 1/2 (x + 3) sin (2x − π) − 1/2 {− 1/2 cos (2x − π) }
= 1/2 (x + 3) sin (2x − π) + 1/4 cos (2x − π)
kalikan 16, tambahkan + C nya
= 16 { 1/2 (x + 3) sin (2x − π) + 1/4 cos (2x − π) } + C
= 8 (x + 3) sin (2x − π) + 4 cos (2x − π) + C
Cara Kedua
16 ∫ (x + 3) cos (2x − π)dx =.....
Langkah Pertama
Buat tabel dua kolom terlebih dahulu seperti berikut

Tempatkan x + 3 di kolom sebelah kiri dan turunkan berturut-turut sampai dapat NOL. Sementara cos (2x − π) di sebelahnya integralkan berturut-turut hingga terakhir sejajar dengan angka nol sebelah kiri.
Kolom pertama
x + 3 jika diturunkan hasilnya adalah 1, dan 1 jika diturunkan hasilnya adalah 0.
Kolom kedua
cos (2x − π) jika diintegralkan hasilnya adalah 1/2 sin (2x − π), kemudian 1/2 sin (2x − π) diintegralkan hasilnya adalah − 1/4 cos (2x − π)
Langkah Kedua
Kalikan baris pertama kolom 1 dengan baris kedua kolom dua, dan
baris kedua kolom 1 dengan baris ketiga kolom 2,
lebih mudahnya ikuti tanda panah yang diberikan gambar diatas, jangan lupa sertakan tanda plus atau minusnya.
Sehingga:
=16 {(x + 3)[1/2 sin (2x − π)] − (1)[− 1/4 cos (2x − π)]} + C
= 8 (x + 3) sin (2x − π) + 4 cos (2x − π) + C
Hasilnya sama dengan cara yang pertama, untuk soal-soal berikutnya akan dipakai cara kedua saja.
Soal No. 2
Hasil dari ∫ 6x(3x − 1)−1/3 dx =.....
A. 3x(3x − 1)2/3 − 3/5 (3x − 1)5/3 + C
B. 4x(3x − 1)2/3 − 6/5 (3x − 1)5/3 + C
C. 9x(3x − 1)2/3 − 6/5 (3x − 1)5/3 + C
D. 4x(3x − 1)2/3 − 3/5 (3x − 1)5/3 + C
E. 3x(3x − 1)2/3 − 6/5 (3x − 1)5/3 + C
Pembahasan
∫ 6x(3x − 1)−1/3 dx

= 6x (1/2 (3x − 1)2/3) − (6)(1/10 (3x − 1)5/3) + C
= 3x (3x − 1)2/3 − 6/10 (3x − 1)5/3 + C
Soal No. 3
Hasil dari ∫ (3x + 2) cos (3x + 2) dx =....
A. (3x + 2) sin (3x + 2) − 3 sin (3x + 2) + C
B. (3x + 2) sin (3x + 2) + 3 sin (3x + 2) + C
C. (2 − 3x) sin (3x + 2) − 3 cos (3x + 2) + C
D. (x + 2/3) sin (3x + 2) − 1/3 cos (3x + 2) + C
E. (x + 2/3) sin (3x + 2) + 1/3 cos (3x + 2) + C
Pembahasan
∫ (3x + 2) cos (3x + 2) dx

= (3x + 2)1/3 sin (3x + 2) + (3) 1/9 cos (3x + 2) + C
= (x + 2/3) sin (3x + 2) + 1/3 cos (3x + 2) + C
Soal No. 4
o∫π x cos x dx = ....
A. − 2
B. − 1
C. 0
D. 1
E. 2
Dicoba dulu, jawabannya adalah A. − 2
Pembahasan
o∫π x cos x dx

= x sin x + cos x ]oπ
= [π sin π + cos π ] − [(0 ) sin 0 + cos 0]
= −1 − 1 = − 2
Soal No. 5
∫ (3x + 1) cos (2x) dx adalah....
A. 1/2 (3x + 1) sin 2x + 3/4 cos 2x + C
B. 1/2 (3x + 1) sin 2x − 3/4 cos 2x + C
C. 1/2 (3x + 1) sin 2x + 3/2 cos 2x + C
D. − 1/2 (3x + 1) sin 2x + 3/2 cos 2x + C
E. − 1/2 (3x + 1) sin 2x − 1/4 cos 2x + C
Kunci : 1/2 (3x + 1) sin 2x + 3/4 cos 2x
Soal No. 6
Hasil dari ∫ x(x + 4)5 dx =....
A. 1/21 (3x + 26)(x + 4)6 + C
B. 1/21 (3x − 14)(x + 4)6 + C
C. 1/21 (3x − 10)(x + 4)6 + C
D. 1/21 (3x + 2)(x + 4)6 + C
E. 1/21 (3x − 2)(x + 4)6 + C
Kunci : 1/21 (3x + 2) (x + 4)6
Soal No. 7
∫ (x2 + 1) cos x dx =......
A. x2 sin x + 2x cos x + C
B. (x2 − 1) sin x + 2x cos + C
C. (x2 + 3) sin x − 2x cos x + C
D. 2x2 cos x + 2x2 sin x + C
E. 2x sin x − (x2 − 1) cos x + C
Kunci jawaban : B. (x2 − 1) sin x + 2x cos + C
Soal No. 8
∫ x(x + 3)4 =.....
A. 1/30 (5x − 3)(x + 3)5 + C
B. 1/30 (3x − 5)(x + 3)5 + C
C. 1/30 (5x + 3)(x + 3)5 + C
D. 1/5 (x − 3)(x + 3)5 + C
E. 1/5 (3 − 5x )(x + 3)5 + C
Misalkan (x + 3) adalah u, dan sisanya, cos (2x − π)dx sebagai dv,
u = (x + 3) ...(Persamaan 1)
dv = cos (2x − π)dx ...(Persamaan 2)
Langkah pertama selesai, kita tengok lagi rumus dasar integral parsial:
∫ u dv = uv − ∫v du
Terlihat di situ kita perlu u, perlu v dan perlu du. u nya sudah ada, tinggal mencari du dan v nya.
Dari persamaan 1, untuk menentukan du, caranya turunkan u nya,
u = (x + 3)
du/dx = 1
du = dx
Dari persamaan 2, untuk menentukan v,
dv = cos (2x − π)dx
atau
dv/dx = cos (2x − π)
dv/dx artinya turunan dari v adalah cos (2x − π), untuk mendapatkan v, berarti kita harus integralkan cos (2x − π) jika lupa, tengok lagi cara integral fungsi trigonometri,
v = ∫ cos (2x − π) dx = 1/2 sin (2x − π) + C
Kita rangkum lagi :
u = (x + 3)
v = 1/2 sin (2x − π)
du = dx
Saatnya kembali ke rumus dasar, masukkan nilai-nilai yang sudah dicari tadi:
16 ∫ (x + 3) cos (2x − π)dx
Simpan dulu 16 nya, terakhir nanti hasilnya baru di kali 16
= uv − ∫v du
= (x + 3) 1/2 sin (2x − π) − ∫ 1/2 sin (2x − π) du
= 1/2 (x + 3) sin (2x − π) − ∫ 1/2 sin (2x − π) dx
= 1/2 (x + 3) sin (2x − π) − 1/2 {− 1/2 cos (2x − π) }
= 1/2 (x + 3) sin (2x − π) + 1/4 cos (2x − π)
kalikan 16, tambahkan + C nya
= 16 { 1/2 (x + 3) sin (2x − π) + 1/4 cos (2x − π) } + C
= 8 (x + 3) sin (2x − π) + 4 cos (2x − π) + C
Cara Kedua
16 ∫ (x + 3) cos (2x − π)dx =.....
Langkah Pertama
Buat tabel dua kolom terlebih dahulu seperti berikut

Tempatkan x + 3 di kolom sebelah kiri dan turunkan berturut-turut sampai dapat NOL. Sementara cos (2x − π) di sebelahnya integralkan berturut-turut hingga terakhir sejajar dengan angka nol sebelah kiri.
Kolom pertama
x + 3 jika diturunkan hasilnya adalah 1, dan 1 jika diturunkan hasilnya adalah 0.
Kolom kedua
cos (2x − π) jika diintegralkan hasilnya adalah 1/2 sin (2x − π), kemudian 1/2 sin (2x − π) diintegralkan hasilnya adalah − 1/4 cos (2x − π)
Langkah Kedua
Kalikan baris pertama kolom 1 dengan baris kedua kolom dua, dan
baris kedua kolom 1 dengan baris ketiga kolom 2,
lebih mudahnya ikuti tanda panah yang diberikan gambar diatas, jangan lupa sertakan tanda plus atau minusnya.
Sehingga:
=16 {(x + 3)[1/2 sin (2x − π)] − (1)[− 1/4 cos (2x − π)]} + C
= 8 (x + 3) sin (2x − π) + 4 cos (2x − π) + C
Hasilnya sama dengan cara yang pertama, untuk soal-soal berikutnya akan dipakai cara kedua saja.
Soal No. 2
Hasil dari ∫ 6x(3x − 1)−1/3 dx =.....
A. 3x(3x − 1)2/3 − 3/5 (3x − 1)5/3 + C
B. 4x(3x − 1)2/3 − 6/5 (3x − 1)5/3 + C
C. 9x(3x − 1)2/3 − 6/5 (3x − 1)5/3 + C
D. 4x(3x − 1)2/3 − 3/5 (3x − 1)5/3 + C
E. 3x(3x − 1)2/3 − 6/5 (3x − 1)5/3 + C
Pembahasan
∫ 6x(3x − 1)−1/3 dx

= 6x (1/2 (3x − 1)2/3) − (6)(1/10 (3x − 1)5/3) + C
= 3x (3x − 1)2/3 − 6/10 (3x − 1)5/3 + C
Soal No. 3
Hasil dari ∫ (3x + 2) cos (3x + 2) dx =....
A. (3x + 2) sin (3x + 2) − 3 sin (3x + 2) + C
B. (3x + 2) sin (3x + 2) + 3 sin (3x + 2) + C
C. (2 − 3x) sin (3x + 2) − 3 cos (3x + 2) + C
D. (x + 2/3) sin (3x + 2) − 1/3 cos (3x + 2) + C
E. (x + 2/3) sin (3x + 2) + 1/3 cos (3x + 2) + C
Pembahasan
∫ (3x + 2) cos (3x + 2) dx

= (3x + 2)1/3 sin (3x + 2) + (3) 1/9 cos (3x + 2) + C
= (x + 2/3) sin (3x + 2) + 1/3 cos (3x + 2) + C
Soal No. 4
o∫π x cos x dx = ....
A. − 2
B. − 1
C. 0
D. 1
E. 2
Dicoba dulu, jawabannya adalah A. − 2
Pembahasan
o∫π x cos x dx

= x sin x + cos x ]oπ
= [π sin π + cos π ] − [(0 ) sin 0 + cos 0]
= −1 − 1 = − 2
Soal No. 5
∫ (3x + 1) cos (2x) dx adalah....
A. 1/2 (3x + 1) sin 2x + 3/4 cos 2x + C
B. 1/2 (3x + 1) sin 2x − 3/4 cos 2x + C
C. 1/2 (3x + 1) sin 2x + 3/2 cos 2x + C
D. − 1/2 (3x + 1) sin 2x + 3/2 cos 2x + C
E. − 1/2 (3x + 1) sin 2x − 1/4 cos 2x + C
Kunci : 1/2 (3x + 1) sin 2x + 3/4 cos 2x
Soal No. 6
Hasil dari ∫ x(x + 4)5 dx =....
A. 1/21 (3x + 26)(x + 4)6 + C
B. 1/21 (3x − 14)(x + 4)6 + C
C. 1/21 (3x − 10)(x + 4)6 + C
D. 1/21 (3x + 2)(x + 4)6 + C
E. 1/21 (3x − 2)(x + 4)6 + C
Kunci : 1/21 (3x + 2) (x + 4)6
Soal No. 7
∫ (x2 + 1) cos x dx =......
A. x2 sin x + 2x cos x + C
B. (x2 − 1) sin x + 2x cos + C
C. (x2 + 3) sin x − 2x cos x + C
D. 2x2 cos x + 2x2 sin x + C
E. 2x sin x − (x2 − 1) cos x + C
Kunci jawaban : B. (x2 − 1) sin x + 2x cos + C
Soal No. 8
∫ x(x + 3)4 =.....
A. 1/30 (5x − 3)(x + 3)5 + C
B. 1/30 (3x − 5)(x + 3)5 + C
C. 1/30 (5x + 3)(x + 3)5 + C
D. 1/5 (x − 3)(x + 3)5 + C
E. 1/5 (3 − 5x )(x + 3)5 + C
Kunci jawaban : A. 1/30 (5x − 3)(x + 3)5 + C
Pembahasan
∫ x(x + 3)4 =.....
∫ x(x + 3)4 =.....
Seperti contoh-contoh sebelumnya:
____________________________________
Turunkan Integralkan
x ----------------\ (+) (x + 3)4
1 -----\ (−) \--------> 1/5 (x + 3)5
0 \------------------> 1/30(x + 3)6
____________________________________
____________________________________
∫ x(x + 3)4
= x/5(x + 3)5 − 1/30(x + 3)6 + C → sampai sini sudah selesai, hanya dipilihan belum nampak, dimodif lagi.
= x/5(x + 3)5 − 1/30(x + 3)(x + 3)5 + C
=[ x/5 − 1/30(x + 3) ] (x + 3)5 + C
= [ x/5 − x/30 − 3/30] (x + 3)5 + C
= [6x/30 − x/30 − 3/30 ] (x + 3)5 + C
= (5x/30 − 3/30)(x + 3)5 + C
= 1/30 (5x − 3)(x + 3)5 + C
Luas Daerah dan Volume Benda Putar
Berikut contoh soal-soal UN materi Luas Daerah dan Volum Benda Putar:
1) UN Matematika SMA 2010 P04 - Kepulauan Riau
Luas daerah yang dibatasi oleh parabola y = 4x − x2, y = −2x + 8, dan sumbu Y adalah....
A. 4 2/3 satuan luas
B. 6 2/3 satuan luas
C. 12 2/3 satuan luas
D. 20 2/3 satuan luas
E. 30 2/3 satuan luas
1) UN Matematika SMA 2010 P04 - Kepulauan Riau
Luas daerah yang dibatasi oleh parabola y = 4x − x2, y = −2x + 8, dan sumbu Y adalah....
A. 4 2/3 satuan luas
B. 6 2/3 satuan luas
C. 12 2/3 satuan luas
D. 20 2/3 satuan luas
E. 30 2/3 satuan luas
2) UN 2010 Yogyakarta
Luas daerah di kuadran I yang dibatasi oleh oleh kurva y = x3, y = x, x = 0 dan garis x = 2 adalah....
A. 2 1/4 satuan luas
B. 2 1/2 satuan luas
C. 3 1/4 satuan luas
D. 3 1/2 satuan luas
E. 4 1/4 satuan luas
3) UN Matematika SMA IPA P04 2010 Kepulauan Riau
Daerah yang dibatasi oleh kurva y = 4 − x2, sumbu X, sumbu Y dan garis x = 1. Volume benda putar yang terjadi jika daerah tersebut diputar mengelilingi sumbu X adalah...
A. 12 8/15 π satuan volum
B. 12 8/12 π satuan volum
C. 13 8/15 π satuan volum
D. 13 8/12 π satuan volum
E. 14 π satuan volum
4) UN Matematika SMA 2010-Yogyakarta
Volume benda putar yang terjadi bila daerah yang dibatasi oleh kurva y = x2 dan daerah y = √x diputar 360° mengelilingi sumbu X adalah....
A. 3/10 π satuan volum
B. 5/10 π satuan volum
C. 1/3 π satuan volum
D. 10/3 π satuan volum
E. 2π satuan volum
5) UN Matematika SMA 2010 P37 Kepulauan Riau
Volume benda putar yang terjadi jika daerah yang dibatasi oleh kurva y = 2x − x2 dan y = 2 − x diputar mengelilingi sumbu X sejauh 360° adalah....
A. 1/5 π satuan volum
B. 2/5 π satuan volum
C. 3/5 π satuan volum
D. 4/5 π satuan volum
E. π satuan volum
6) UN 2011 Paket 12 Yogyakarta
Volume benda putar jika daerah yang dibatasi oleh kurva y = x2, garis y = 2x di kuadran I diputar 360° terhadap sumbu X adalah....
A. 20/15 π satuan volum
B. 30/15 π satuan volum
C. 54/15 π satuan volum
D. 64/15 π satuan volum
E. 144/15 π satuan volum
Pembahasan Soal Nomor 2
Sketsa grafik yang dibentuk oleh kedua fungsi, cari titik potong y = x3 dan y = x
Titik potong :
x3 = x
x3 − x = 0
x(x2 − 1) = 0
x(x − 1)(x + 1) = 0
x = 0 v x = 1 v x = − 1
Karena dibatasi juga oleh garis x = 0, maka titik potong yang digunakan adalah 0 dan 1 saja. Berikut sketsa kasar grafiknya:

Dari sketsa grafik terlihat dua area yang harus dicari luasnya, area pertama dibatasi oleh 0 dan 1, area kedua dibatasi oleh 1 dan 2 selengkapnya perhitungan mencari luasnya sebagai berikut:
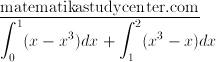
Kita hitung secara terpisah saja untuk mengurangi resiko kesalahan perhitungan akibat kurangnya ketelitian
Luas area pertama
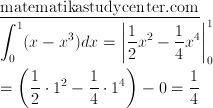
Luas area kedua
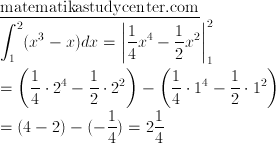
Jumlahkan
2 1/4 + 1/4 = 2 1/2 satuan luas
Pembahasan Soal No. 5
Sketsa grafiknya. cari titik-titik potong:
2x − x2 = 2 − x
2x − x2 + x − 2 = 0
x2 − 3x + 2 = 0
(x − 2)(x−1) = 0
x = 2 v x = 1
Berikut sketsa kasar grafik selengkapnya
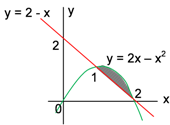
Waktunya berhitung:
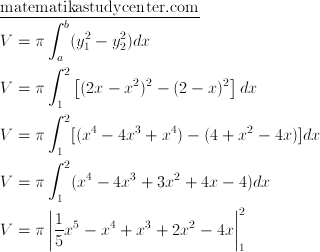
Eksekusi akhir
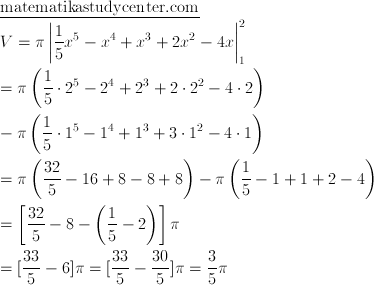
Volume Benda Putar Sumbu Y
Berikut ini contoh soal integral volume benda putar pada sumbu y:
Soal
Volume benda putar jika daerah yang dibatasi kurva y = − x2 + 4 dan y = − 2x + 4 diputar 360° mengelilingi sumbu Y adalah.....
A. 8 π satuan volume
B. 13/2 π satuan volume
C. 4 π satuan volume
D. 8/3 π satuan volume
E. 5/4 π satuan volume
(Sumber Soal : UN Matematika SMA Tahun 2007)
Volume benda putar jika daerah yang dibatasi kurva y = − x2 + 4 dan y = − 2x + 4 diputar 360° mengelilingi sumbu Y adalah.....
A. 8 π satuan volume
B. 13/2 π satuan volume
C. 4 π satuan volume
D. 8/3 π satuan volume
E. 5/4 π satuan volume
(Sumber Soal : UN Matematika SMA Tahun 2007)
Pembahasan
Langkah pertama yang biasa ditempuh adalah membuat sketsa grafik kurva-kurva yang terlibat agar nampak batas-batas yang akan diambil,
Langkah pertama yang biasa ditempuh adalah membuat sketsa grafik kurva-kurva yang terlibat agar nampak batas-batas yang akan diambil,
Kurva pertama bentuknya persamaan kuadrat,
y = −x2 + 4
Cari titik potong pada sumbu x, berarti y diberi harga nol, y = 0
y = −x2 + 4
0 = −x2 + 4
0 = 4 −x2
Faktorkan,
0 = (x + 2)(x − 2)
x = − 2 atau x = 2
Titik-titik yang diperoleh dari langkah ini adalah (2, 0) dan titik (−2, 0)
Titik potong pada sumbu y, berarti x diberi harga nol, x = 0
y = −x2 + 4
y = −02 + 4
y = 4
Titik yang diperoleh dari langkah ini adalah (0, 4)

Kurva Kedua berbentuk persamaan linier
y = − 2x + 4
Titik potong sumbu x, berarti y = 0
y = − 2x + 4
0 = − 2x + 4
2x = 4
x = 4/2 = 2
Diperoleh titik (2, 0)
Titik potong sumbu y, berarti x = 0
y = − 2x + 4
y = − 2(0) + 4
y = 4
Diperoleh titik (0, 4)
Grafik selengkapnya sebagai berikut

Menentukan Batas-batas
Jika diputar pada sumbu x, terlihat dari gambar batas-batasnya adalah 0 dan 2
Jika diputar pada sumbu y, terlihat batas-batasnya adalah 0 dan 4
Kali ini akan dihitung untuk putar sumbu y, sehingga batas yang diambil 0 dan 4
Dari rumus volume benda putar pada sumbu y untuk dua buah kurva:
V = π a∫b ( [f1(y)]2 − [f2(y)]2 ) dy
atau
V = π a∫b ( [x1]2 − [x2]2 ) dy
→ Ubah bentuk "y =... " menjadi "x =..." atau "x2 =..." ,
y = −x2 + 4
x2 = 4 − y
y = − 2x + 4
2x = 4 − y
x = 2 − 1/2 y
x2 = 4 −2y + y2/4
sehingga
V = π a∫b ( [x1]2 − [x2]2 ) dy
V = π 0∫4 ( [4 − y] − [4 −2y + y2/4] ) dy
V = π 0∫4 ( 4 − y − 4 + 2y − y2/4 ) dy
V = π 0∫4 (y − y2/4 ) dy
V = π [ 1/2 y2 − y3/12]04
V = (1/2 . 16 − 64/12)π − (0) π = 8/3 π
Soal
Perhatikan gambar diarsir di samping!

Jika daerah yang diarsir diputar mengelilingi sumbu Y, maka volume benda putar yang terjadi adalah….
A. 6 2/5 π satuan volume
B. 8 π satuan volume
C. 13 2/3 π satuan volume
D. 15 1/3 π satuan volume
E. 25 3/5 π satuan volume
y = −x2 + 4
Cari titik potong pada sumbu x, berarti y diberi harga nol, y = 0
y = −x2 + 4
0 = −x2 + 4
0 = 4 −x2
Faktorkan,
0 = (x + 2)(x − 2)
x = − 2 atau x = 2
Titik-titik yang diperoleh dari langkah ini adalah (2, 0) dan titik (−2, 0)
Titik potong pada sumbu y, berarti x diberi harga nol, x = 0
y = −x2 + 4
y = −02 + 4
y = 4
Titik yang diperoleh dari langkah ini adalah (0, 4)

Kurva Kedua berbentuk persamaan linier
y = − 2x + 4
Titik potong sumbu x, berarti y = 0
y = − 2x + 4
0 = − 2x + 4
2x = 4
x = 4/2 = 2
Diperoleh titik (2, 0)
Titik potong sumbu y, berarti x = 0
y = − 2x + 4
y = − 2(0) + 4
y = 4
Diperoleh titik (0, 4)
Grafik selengkapnya sebagai berikut

Menentukan Batas-batas
Jika diputar pada sumbu x, terlihat dari gambar batas-batasnya adalah 0 dan 2
Jika diputar pada sumbu y, terlihat batas-batasnya adalah 0 dan 4
Kali ini akan dihitung untuk putar sumbu y, sehingga batas yang diambil 0 dan 4
Dari rumus volume benda putar pada sumbu y untuk dua buah kurva:
V = π a∫b ( [f1(y)]2 − [f2(y)]2 ) dy
atau
V = π a∫b ( [x1]2 − [x2]2 ) dy
→ Ubah bentuk "y =... " menjadi "x =..." atau "x2 =..." ,
y = −x2 + 4
x2 = 4 − y
y = − 2x + 4
2x = 4 − y
x = 2 − 1/2 y
x2 = 4 −2y + y2/4
sehingga
V = π a∫b ( [x1]2 − [x2]2 ) dy
V = π 0∫4 ( [4 − y] − [4 −2y + y2/4] ) dy
V = π 0∫4 ( 4 − y − 4 + 2y − y2/4 ) dy
V = π 0∫4 (y − y2/4 ) dy
V = π [ 1/2 y2 − y3/12]04
V = (1/2 . 16 − 64/12)π − (0) π = 8/3 π
Soal
Perhatikan gambar diarsir di samping!

Jika daerah yang diarsir diputar mengelilingi sumbu Y, maka volume benda putar yang terjadi adalah….
A. 6 2/5 π satuan volume
B. 8 π satuan volume
C. 13 2/3 π satuan volume
D. 15 1/3 π satuan volume
E. 25 3/5 π satuan volume
Pembahasan
y = √x
y2 = x
y4 = x2
x2 = y4
y = √x
y2 = x
y4 = x2
x2 = y4
Dari rumus volume benda putar pada sumbu y untuk satu buah kurva:
V = π o∫2 x2 dy
V = π o∫2 y4 dy
V = π [ 1/5 y5 ]02 = 1/5 π [ y5 ]02
V = 1/5 π [ (25) − (05) ] = 32/5 π = 6 2/5 π satuan volume
V = π o∫2 x2 dy
V = π o∫2 y4 dy
V = π [ 1/5 y5 ]02 = 1/5 π [ y5 ]02
V = 1/5 π [ (25) − (05) ] = 32/5 π = 6 2/5 π satuan volume
Soal
Volume benda putar yang terbentuk dari daerah yang di kuadran I yang dibatasi oleh kurva x = 2√2 y2, sumbu Y, dan lingkaran x2 + y2 = 9, diputar mengelilingi sumbu Y adalah....
A. 106/15 π satuan volume
B. 124/15 π satuan volume
C. 146/15 π satuan volume
D. 164/15 π satuan volume
E. 248/15 π satuan volume
Pembahasan
Volume benda putar pada sumbu Y.
Kurva I
x = 2√2 y2
x2 = 8y4
Kurva II
x2 + y2 = 9
x2 = 9 − y2
Tentukan titik potongnya dulu
8y4 = 9 − y2
8y4 + y2 − 9 = 0
Faktorkan
(8y2 + 9)(y2 - 1) = 0
Ambil y2 - 1 = 0
y2 = 1→ y = ± 1
Sketsa kasar grafiknya sebagai berikut:

Terlihat Volumenya

Volume benda putar yang terbentuk dari daerah yang di kuadran I yang dibatasi oleh kurva x = 2√2 y2, sumbu Y, dan lingkaran x2 + y2 = 9, diputar mengelilingi sumbu Y adalah....
A. 106/15 π satuan volume
B. 124/15 π satuan volume
C. 146/15 π satuan volume
D. 164/15 π satuan volume
E. 248/15 π satuan volume
Pembahasan
Volume benda putar pada sumbu Y.
Kurva I
x = 2√2 y2
x2 = 8y4
Kurva II
x2 + y2 = 9
x2 = 9 − y2
Tentukan titik potongnya dulu
8y4 = 9 − y2
8y4 + y2 − 9 = 0
Faktorkan
(8y2 + 9)(y2 - 1) = 0
Ambil y2 - 1 = 0
y2 = 1→ y = ± 1
Sketsa kasar grafiknya sebagai berikut:

Terlihat Volumenya



Komentar
Posting Komentar